The PC game Factorio presents an interesting optimisation problem which I’ve been using to improve my python-thinking: how to optimally lay down structures in the game, with a series of overlapping constraints.
Background
Factorio is a resource management and logistics sandbox game on the PC [https://factorio.com/] which asks the player to place structures which obtain resources, and then process them into increasingly complex products.
One of those products is oil, which is obtained from randomly occuring pools within small areas on the world map:

The player uses 5 structures to collect and distribute the oil:

Pumpjacks are placed on the oil, and have 4 possible orientations (the cardinal directions). Oil must be piped from these structures and pipes connect to a single location (which changes for each of the 4 rotations.

Beacons are late-game structures which provide benefits to other structures within a certain range. Without dwelling on the detail, it is desirable to have as many of these covering each pumpjack as possible. They occupy 3 squares, but the beneficial effect stretches a further 3 in each direction, so 9×9 in total (see below for some examples).

Power poles are needed to provide electricity to the pumpjacks and beacons. They need to be close enough to each other to be connected to the grid, and they broadcast power in an area around them. There are 4 different kinds, but the concept is the same for each.

Pipes (x2) either run above ground, or underground. Oil must be piped away from the oilfield to be useful.
The problem
Given an arbitrary layout of oil on the map, what is the most efficient layout of structures so that:
- All oil is pumped
- All buildings are powered
- All pumpjacks are covered by the largest possible number of beacons
I know of at least one tool which already proposes this, I’m interested in going through the exercise myself, partly to give me a real world problem to practice my Python, and also to see if I can do better!
Part 1: Where to put the Beacons
I want to start backwards, with the purest version of the problem. Given a set of pumps, how do we decide where to put beacons.

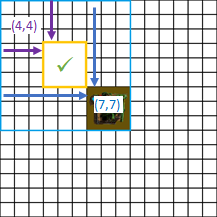
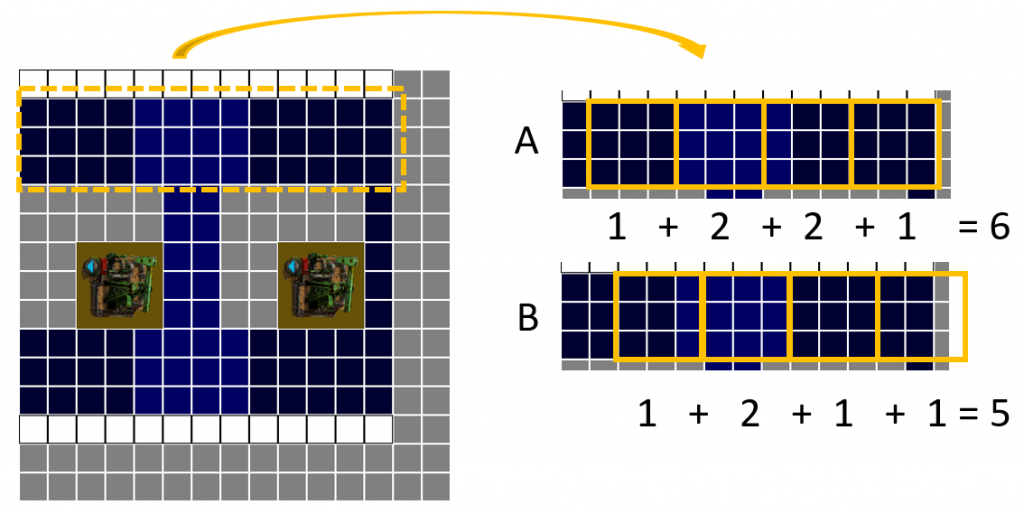
For simplicity, let’s refer to an objects placement by the top leftest square it occupies, so the example above has a pump at location (7,7), and the beacon is at (4,4). In the code, I’ll use arrays, so these locations would be [6,6] and [3,3], starting from the 0 base.
We can then draw out a heatmap of the ‘valid’ placements for the beacon around this single pump

A beacon placed in any of the blue squares would be a valid placement, because there is only a single pump, there is no difference in the value of each square.

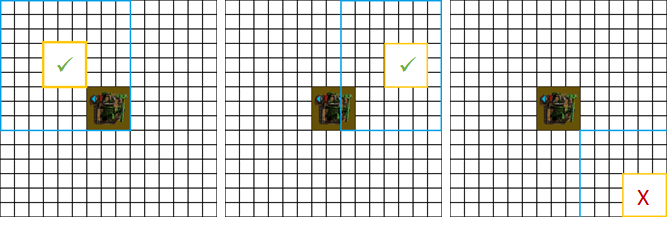
Adding a second pump gives a new dimension to the problem, the lighter blue squares are beacons which would affect both the pumps. Our first priority should be to make sure we cover as many of these cells as possible, and, we must avoid ‘blocking’ these more valuable cells by placing a beacon in lower value adjacent cells
There’s also a more subtle ‘blocking’ which can occur if a beacon is placed in a high value cell which stops another being available
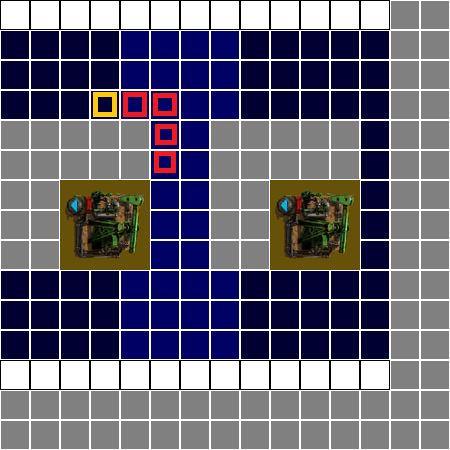
In this example, starting the beacons in cell 4 would reduce the overall coverage by 1. Despite each cell having the same ability to cover both beacons
In this example, we can place the same number of beacons.. but.. they may not be as valuable.

In this final example, the central square has value 12, that seems like an obvious place to put a beacon, but it would prevent any other squares being used:

A more optimal solution places 4 lower value beacons, which sum to a greater amount
There is a hidden cost of choosing cell, in that it prevents it’s neighbours being used. This could make it less valuable to our overall solution. We need to find a way to discount cells which lead to this blocking.
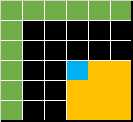
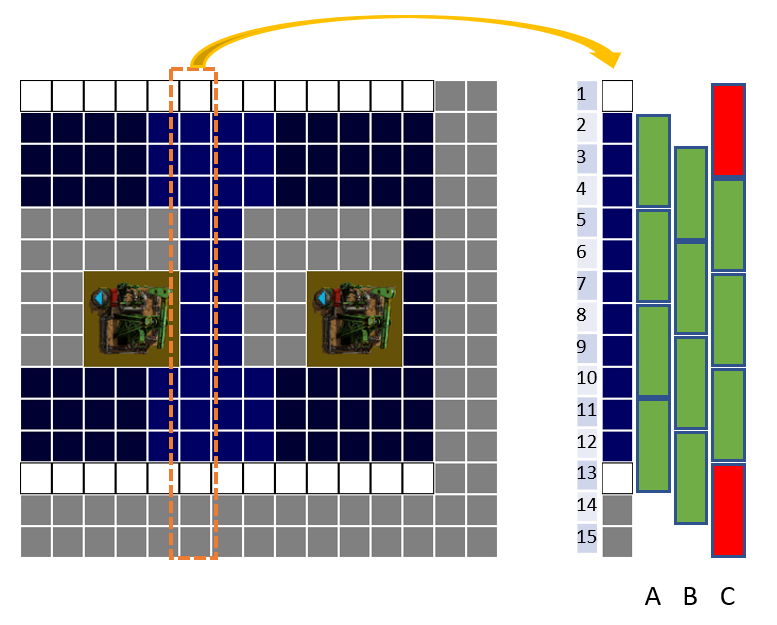
In order to correctly assess the opportunity cost of any square choice, we need to look at the best combination it enables, minus the best combination it blocks. First we loop through all the ‘cost’ combinations and take the one which gives the highest value
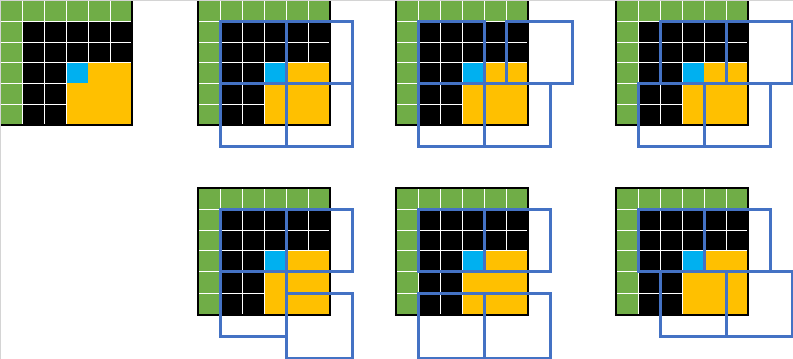
Then we loop through the smaller number of green cell combinations which are the possibilities not blocked by the choice of blue square, and take the best combination which is not blocked – the ‘benefit’ of choosing that square
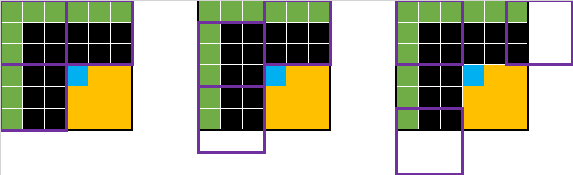
I’ve then subtracted the highest cost from the highest benefit, and calculate the benefit-cost = Opportunity Cost for each square.
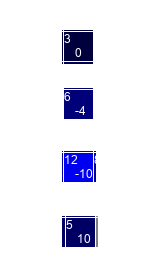
Each cell now has 2 important values:
Top left is the ‘Value‘ of the cell – how many pumps the beacon would be able to influence
Bottom right is the ‘Opportunity Cost‘ – the benefit of the cell, minus the cost. Where the cost is negative, the cell is worth less than the cells it blocks, where it’s positive, the cell provides more benefit than it removes
(A cell can have a bigger positive than it’s own value because of the other squares it enables, I’m not 100% sure that logic works, but I think I can account for that in the implementation)

A heatmap of the raw values 
A heatmap of the opportunity cost
Now we can loop through the grid, finding the highest Opportunity Benefit square, placing a beacon on it, then recalculating and repeating.
And finally, after all that, here’s what it does:

I’m left a bit unsure. The final arrangement has some glitches, like 4,5,9 being offset from 11, 14 – this is due to the way I’m looping through the grid when checking for the best Opp-Benefit. But there’s a general sense that, while my logic feels sound, I’m not able to prove the best-ness of the solution.
Anyway. This is the end of part 1. My next options are either going back and fixing up the code (which I’ll do before I share anything), or moving on to the other constraints.
Good job Alex, I love your research into this. I feel all of us do these calculations in our head when placing beacons, but creating a program that does it is awesome.