‘Cheating’ at Tuble

Since Wordle took the world by storm, a large number of innovative clones have emerged, one which I was pointed to recently is Tuble, where the aim is to guess the correct Tube Station in as few attempts as possible.

Once the initial fun dies down, I’ve quite enjoyed looking at these games as analytical puzzles, and finding an algorithm to solve them.

The Problem

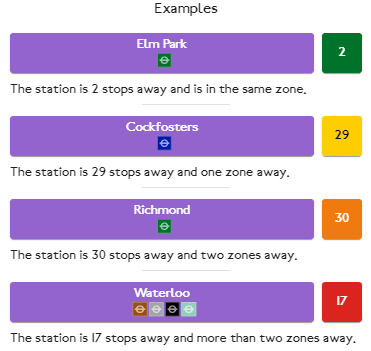
As you make guesses, the game returns two data points to help you refine the next guess. The colour of the blob tells you how many zones are between the guess and the answer, and the number is how many station stops it would take to get there.

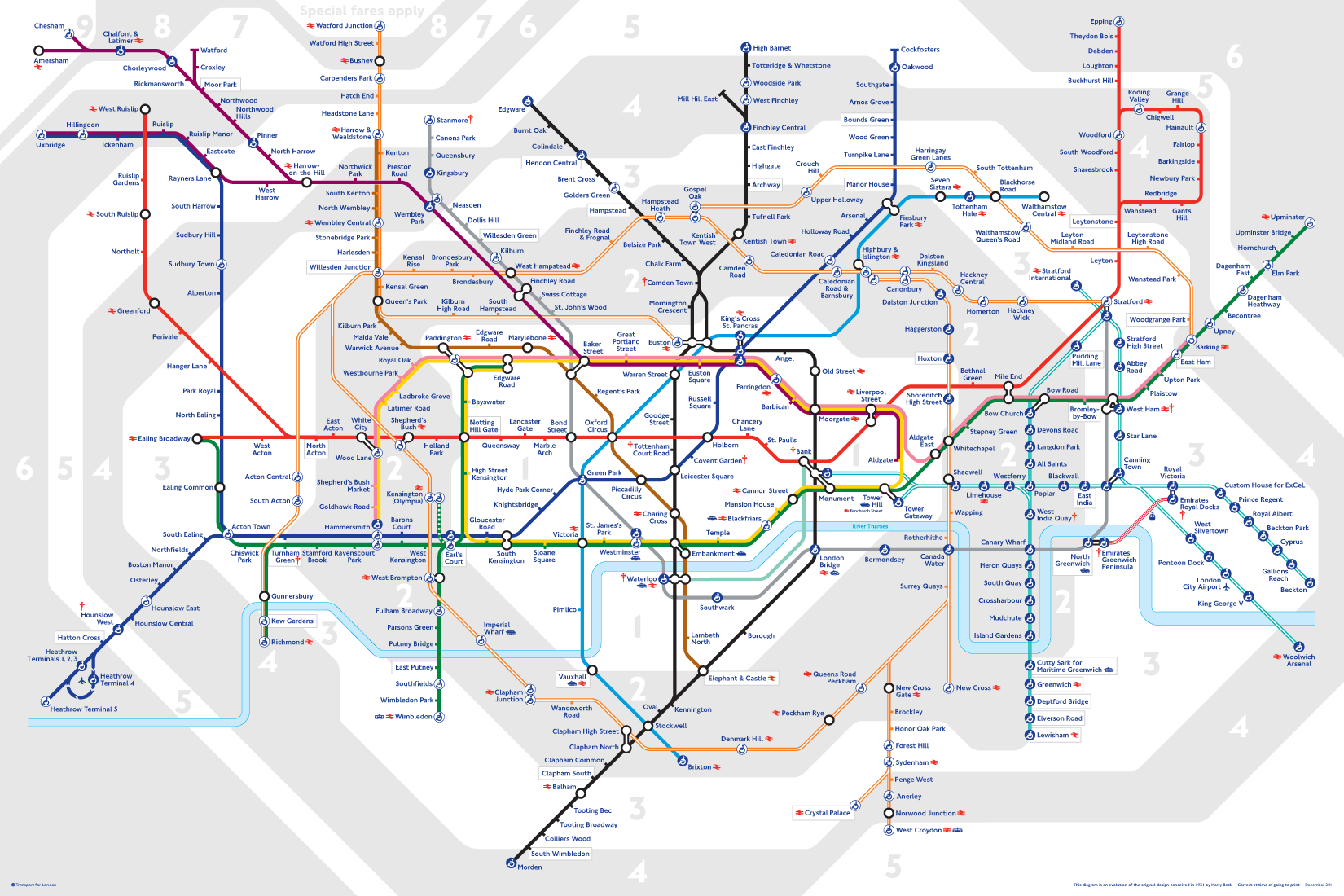
Tube map | Transport for London — This belongs to TFL

The Tube map is pretty well known, especially for Londoners, and the game only includes the core tube (no DLR, no TFL Rail, and also no Crossrail). Turning the map into data is a graph problem, and the biggest hurdle is turning the picture above into a collection of node and edge data.

The solution

Get the station data into Python
Determine the possible answers given guess(es) made
Determine the next best guess

1. Getting the data into Python

A quick google pointed me to this blog post (thanks Mark Dunne!), Mark had already found this github repo (thanks Nicola!) which had pre-built csvs with the info needed to build a networkx graph representation of the tube.

connections = pd.read_csv('london.connections.csv')

#filter out DLR
connections=connections[connections['line']!=13] 
connections=connections[connections['line']!=5]

station1=connections["station1"]
station2=connections["station2"]
stationMasterList=list(set(pd.concat([station1, station2]).to_list()))

stations=stations[stations.index.isin(stationMasterList)]

This first step removes the DLR and ELL stations (which aren’t in the game)

Then I’ve shamelessly copy-pasted this code from Mark’s notebook

graph = nx.Graph()

for connection_id, connection in connections.iterrows():
    station1_name = stations.loc[connection['station1']]['name']
    station2_name = stations.loc[connection['station2']]['name']
    graph.add_edge(station1_name, station2_name, time = connection['time'])
    
#add the connection between Bank and Monument manually
graph.add_edge('Bank', 'Monument', time = 1)

I’ve now got a graph with all my stations (nodes) and lines (edges).

2. Determine the possible answers given a guess

I’m not sure if there’s a more efficient way to do this, but the first iteration is just a loop through all the stations in the graph, and adding them to a list if they meet the conditions of the last guess.

def getPossiblesList(startStation, maxDistance, zoneFlag): #zoneFlag takes values as: green=0, yellow=1, orange=2, red=3
    startZone=stations[stations["name"]==startStation]["zone"].item()
    returnList=[]
    for id, stat in stations['name'].iteritems():
        if len(nx.shortest_path(graph, startStation, stat))-1 == maxDistance:
            details = stations[stations["name"]==stat][["name", "zone", ]].to_records(index=False)
            name=details[0][0]
            zone=details[0][1]
            if zoneFlag==0:
                if startZone==zone:
                    returnList.append(name)
            if zoneFlag==1:
                if abs(zone-startZone)>=1 and abs(zone-startZone)<2:
                    returnList.append(name)
            if zoneFlag==2:
                if abs(zone-startZone)>=2 and abs(zone-startZone)<3:
                    returnList.append(name)
            if zoneFlag==3:
                if abs(zone-startZone)>=3:
                    returnList.append(name)
    return returnList

My first guess is 16 stops from the correct station, and 1 zone away (plus or minus), given that, here are the possible stations which meet the criteria

['Holloway Road', 'Bethnal Green', 'Finsbury Park', 'Chalk Farm', 'Kentish Town', 'Bermondsey']

This is probably something you could do in your head, and leaves a much reduced number of possible options

3. Determine the next best guess

It will almost always be best to guess one of the stations in the shortlist, but there may be a better guess which limits the possible options more

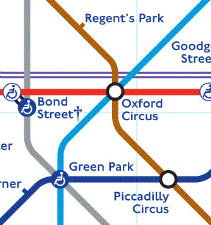
E.g. if the possible stations are Regent’s Park or Piccadilly Circus, a guess of Oxford Circus wouldn’t help atall. Green Park would be better as you’d know exactly which station was right based on the feedback

However, given there are only 2 options, it would be much more sensible to guess one of those options as you’ve got a 50% chance of ‘getting lucky’.

Gut feel is that there could be an edge case where guessing from the shortlist would risk you getting less information than a non-shortlist station, in which case you’d be gambling a possible win on the next turn, vs a definite win on a subsequent turn.

def tubleResult(startStation, endStation):
    path=len(nx.shortest_path(graph, startStation, endStation))-1 #minus one as both stations are included in the result
    startZone=stations[stations["name"]==startStation]["zone"].item()
    endZone=stations[stations["name"]==endStation]["zone"].item()

    if abs(endZone-startZone)<1.0:
        zoneFlag=0
    elif abs(endZone-startZone)>=1 and abs(endZone-startZone)<2:
        zoneFlag=1
    elif abs(endZone-startZone)>=2 and abs(endZone-startZone)<3:
        zoneFlag=2
    elif abs(endZone-startZone)>=3:
        zoneFlag=3
    return(path, zoneFlag) #zoneFlag takes values as: green=0, yellow=1, orange=2, red=3

This code returns the values which the game would give you if you guessed a ‘start station’ and the correct result was ‘end station’. Using this, I can compare the information I’d get from using different guesses and select the one with the least ambiguous outcome.

fullList=[] #a full list of the stations, for the case where there are no previous guesses
for id, stat in stations['name'].iteritems():
    fullList.append(stat)

guesslist=[]
guesslist.append(('Ealing Broadway', 16, 1)) #Station name, number of stops away, encoded colour of the tile

returnLists=[] #store all the possible answers, based on guesses
for guess in guesslist:
    returnLists.append(getPossiblesList(guess[0], guess[1], guess[2]))

remainderList=[] #this will store a unique/deduped list of stations
if len(returnLists)==0:
    remainderList=list(set(fullList)) #clumsy dedup
else:
    remainderList=list(set.intersection(*[set(list) for list in returnLists])) #funky bit of code which I hope gives me the intersection of all results
    print(remainderList)

In the absence of a proper UI, the user adds more lines to the ‘guessList’, and the code runs from that.

if len(remainderList)==1:
    print ("The answer is "+remainderList[0])
if len(remainderList)==2:
    print ("The answer is either "+remainderList[0] +" or "+remainderList[1])
else:
    #Remainder List Loop
    bestDiff=1000
    bestStation=""
    for guessStat in remainderList:
        outcomes=[]
        for remainderStat in remainderList:
            outcomes.append(tubleResult(guessStat, remainderStat))
        numOutcomes=len(outcomes)

        numUniqueOutcomes=len(set(outcomes))
        diff=numOutcomes-numUniqueOutcomes
        if diff<bestDiff:
            bestDiff=diff
            bestStation=guessStat

    #Full List Loop
    for guessStat in fullList:
        outcomes=[]
        for remainderStat in remainderList:
            outcomes.append(tubleResult(guessStat, remainderStat))
        numOutcomes=len(outcomes)

        numUniqueOutcomes=len(set(outcomes))
        diff=numOutcomes-numUniqueOutcomes
        if diff<bestDiff:
            bestDiff=diff
            bestStation=guessStat

    print('The best guess is ' +bestStation +" with a duplication of "+ str( bestDiff))

This block of code will return one of 3 outcomes, a single result, a pair, or the best guess. I loop the final step first through the remainder list, then through all stations. If no station gives more information than one on the remainder list, I’d rather pick from that list – just in case I get lucky!

The performance

It works!

Alex’s Blog

Whatever I’m thinking about