We recently welcomed our second son into the world, and while my wife waited for a labour room to become free, we discussed the complexity of deciding how many rooms any given hospital must need. I wondered about the information available, and how they can prepare for spikes.. and that got me thinking about how to model it.. so here goes

I’ll be including good and bad outcomes of the pregnancy journey – please consider if you’re comfortable reading that before you continue.

The problem

A human pregnancy lasts around 40 weeks. Most babies arrive between 38 and 42, but there are lots of reasons why a baby can arrive earlier than that. In the UK, mothers to be are offered a range of options for where they would like to have their baby, roughly: Home Birth, Midwife-lead units, Labour wards.

Some of the home births end up moving to a medical setting due to complications, but most women who give birth in hospital will head there when they’re in established labour. A small proportion (including my wife) will be induced for various reasons, and they’re admitted before labour starts.

There are a limited number of rooms available in any labour ward (more so since Covid, as hospitals have typically set up quarantine rooms form mums-to-be who have the virus). It’s not immediately clear how much pressure these rooms are under as the overlapping situations for each mother vary.

I want to start with an agent-based approach:

1. Creating new Women at a rate which is consistent with UK stats
2. Simulating the success rates for each as they progress
3. Simulating a start of labour (again, consistent with the distributions in the real world)
4. Simulating a total time needed in a room to give birth, and rest afterwards

I can then analyse these stats to see how many rooms would be needed.

Step 1. Women

Find more statistics at Statista

There are lots of useful stats available for this project, starting with the above, which I can piece together. As a starting point, I’m going to choose a population size, then assign them ages which match the UK distribution.

I’ll then run the population over a period of time, by day, giving each a probability of falling pregnant, then for those who are, running the course of each pregnancy to get my outcome.

class Woman:
    ageYears: int
    ageDays: int
    pregnant:bool
    conceptionDt: datetime
    dueDt: datetime
    termWeeks: int
    termDays: int
    formerPregnancies: list
    labourList: list

    def __init__(self, _age):
        self.pregnant=False
        self.ageYears=_age
        self.ageDays=0
        self.formerPregnancies=[]
        self.labourList=[]

Part of the point of this is to get some stats at the end, so along with some obvious properties, I’ve got a couple of lists to store the results of previous pregnancies, and the details of each simulated labour.

2. Simulating success rates

Again, content warning here, I’m not being gruesome, but having kids isn’t always smooth sailing.

My simulation starts with an almost unknown commodity, the day of conception. Practically it’s almost impossible to know this, but it exists.

From the point of (simulated) pregnancy, there are a set of outcomes I’m allowing by probability.

1. Miscarriage – loss of a pregnancy in the first 20 weeks
2. Termination – decision to end the pregnancy within the first 26 weeks
3. Birth – entering labour and delivering a baby

Much, much more depth could exist here, but I think this will be enough to give me the data I want.

3. Simulating start of labour

This is probably the most interesting bit for my problem, but I like the idea of the having more accuracy behind it. Modelling the ages, and age related outcomes gives me more nuance in the analysis at the end.

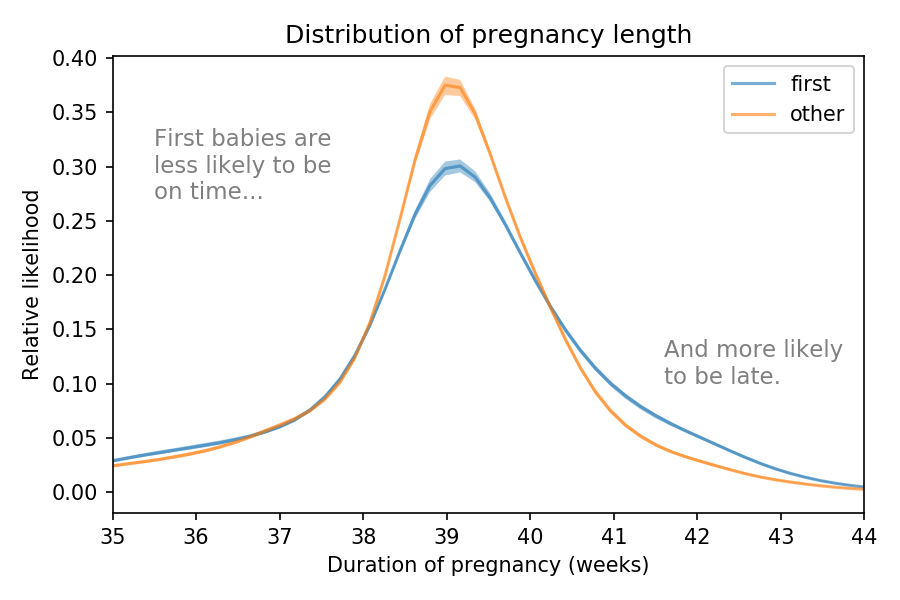
It’s this distribution which started me wondering about the way this would play out across a bigger population, and therefore how confident the NHS can be about the number of labour rooms.

4. Total time in labour

def labourStageCalcs(_ageYears, _termWeeks, _date):
    offset=randint(0,23) #pick a random hour of the day for things to kick-off
    DT=datetime.datetime.combine(_date, datetime.datetime.min.time())
    
    firstLatentStageStDT=DT+timedelta(hours=offset) #Start of contractions
    lenFirstLatent=gauss(12,4) #assume mean 12h, SD 4
    
    firstActiveStageStDT=firstLatentStageStDT+timedelta(hours=lenFirstLatent) #Start of active labour
    lenFirstActive=gauss(6,2)
    
    secondStageStDT=firstActiveStageStDT+timedelta(hours=lenFirstActive) #Start of 'pushing'
    lenSecond=gauss(1,0.5)
    
    thirdStageStDT=secondStageStDT+timedelta(hours=lenSecond) #Baby is born, the cleanup begins
    thirdStageEnDT=thirdStageStDT+timedelta(hours=6) #Give each women 6 hours in the room to recover

    return firstLatentStageStDT, firstActiveStageStDT, secondStageStDT, thirdStageStDT,thirdStageEnDT

At this stage, I just want something which works, no nuance by age/etc

The results

Assuming a female population of 200k, with no current pregnancies, run for 720 days, this show the ramp up of pregnancies

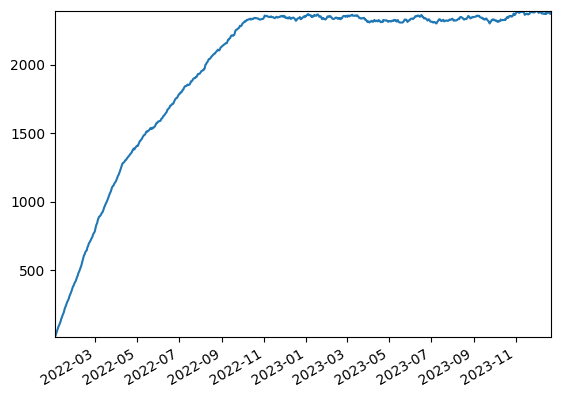
Around 9 months later, the population hit’s a steady state with around 2.3k women pregnant at any time.

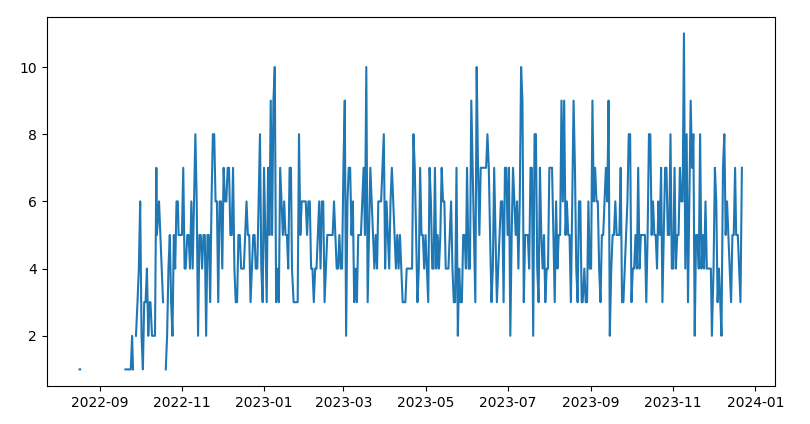
This shows a daily view of the maximum number of beds occupied at any time

And here as a table. The average (mean and median) is 5, with only 5 days needing 10 or more, and only one needing 11 – the highest on any given day

This answers most of my original question. Given a known population, it’s not a big surprise that the number of pregnant women hits a fixed level – I’ve created that by adding a constant number (based on the UK population rate). It’s more interesting that the randomness surrounding the actual birth still results in a number of rooms which can be estimated ahead of time with reasonable confidence.

In future iterations, I’d like to look at the data which would be available to the hospital ahead of time, and maybe add some more variability based on things like age.